Vimos em aula que
O polinômio de Taylor da 
de ordem 
é dado abaixo
 = `+`(1, x, `/`(`*`(`^`(x, 2)), `*`(factorial(2))), `/`(`*`(`^`(x, 3)), `*`(factorial(3))), `/`(`*`(`^`(x, 4)), `*`(factorial(4))), ` . . . `, `/`(`*`(`^`(x, n)), `*`(factorial(n))))](images/Expo_0_5.gif){kind=small}
=
.
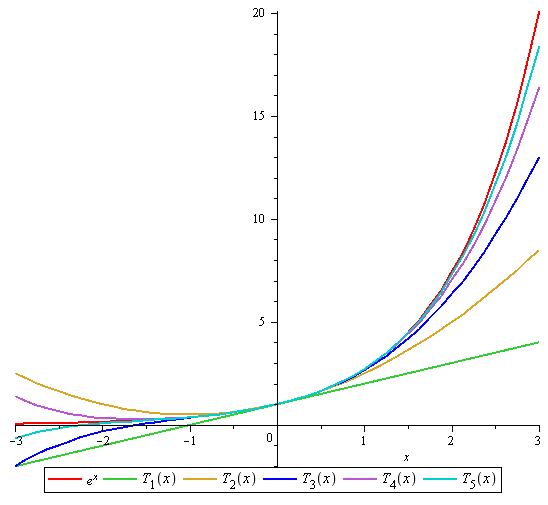
Os polinômios de Taylor de ordem de 1 a 5 são descritos a seguir
 = 1](images/Expo_0_7.gif){kind=small} |
|
 = `+`(1, x)](images/Expo_0_8.gif){kind=small} |
|
 = `+`(1, x, `*`(`/`(1, 2), `*`(`^`(x, 2))))](images/Expo_0_9.gif){kind=small} |
|
 = `+`(1, x, `*`(`/`(1, 2), `*`(`^`(x, 2))), `*`(`/`(1, 6), `*`(`^`(x, 3))))](images/Expo_0_10.gif){kind=small} |
|
 = `+`(1, x, `*`(`/`(1, 2), `*`(`^`(x, 2))), `*`(`/`(1, 6), `*`(`^`(x, 3))), `*`(`/`(1, 24), `*`(`^`(x, 4))))](images/Expo_0_11.gif){kind=small} |
|
 = `+`(1, x, `*`(`/`(1, 2), `*`(`^`(x, 2))), `*`(`/`(1, 6), `*`(`^`(x, 3))), `*`(`/`(1, 24), `*`(`^`(x, 4))), `*`(`/`(1, 120), `*`(`^`(x, 5))))](images/Expo_0_12.gif){kind=small} |
(1) |
Graficamente, termos
| > | ![`assign`(i, 'i'); -1; `assign`(n, 'n'); -1; plot([exp(x), seq(sum(`/`(`*`(`^`(x, i)), `*`(factorial(i))), i = 0 .. n), n = 1 .. 5)], x = -3 .. 3, thickness = 2); 1](images/Expo_0_13.gif){kind=small} |
 |
| > |
| > |
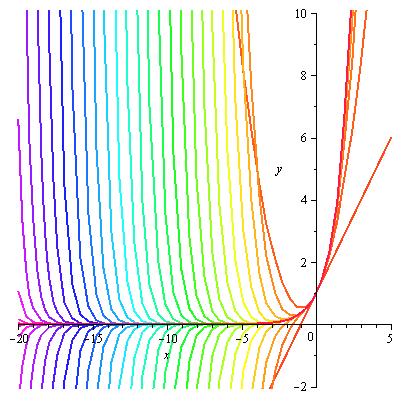
A seguir, temos uma ilustração quando determinamos os polinômios com ordem variando de 1 a 60.
| > | ![`assign`(m, 60); 1; `assign`(frms, seq(plot([exp(x), convert(taylor(exp(x), x, i), polynom)], x = -20 .. 5, y = -2 .. 10, color = [red, COLOR(HUE, `/`(`*`(i), `*`(`+`(m, 2))))], thickness = 2), i = 2 ...](images/Expo_0_15.gif){kind=small} ![`assign`(m, 60); 1; `assign`(frms, seq(plot([exp(x), convert(taylor(exp(x), x, i), polynom)], x = -20 .. 5, y = -2 .. 10, color = [red, COLOR(HUE, `/`(`*`(i), `*`(`+`(m, 2))))], thickness = 2), i = 2 ...](images/Expo_0_16.gif){kind=small} ![`assign`(m, 60); 1; `assign`(frms, seq(plot([exp(x), convert(taylor(exp(x), x, i), polynom)], x = -20 .. 5, y = -2 .. 10, color = [red, COLOR(HUE, `/`(`*`(i), `*`(`+`(m, 2))))], thickness = 2), i = 2 ...](images/Expo_0_17.gif){kind=small} ![`assign`(m, 60); 1; `assign`(frms, seq(plot([exp(x), convert(taylor(exp(x), x, i), polynom)], x = -20 .. 5, y = -2 .. 10, color = [red, COLOR(HUE, `/`(`*`(i), `*`(`+`(m, 2))))], thickness = 2), i = 2 ...](images/Expo_0_18.gif){kind=small} ![`assign`(m, 60); 1; `assign`(frms, seq(plot([exp(x), convert(taylor(exp(x), x, i), polynom)], x = -20 .. 5, y = -2 .. 10, color = [red, COLOR(HUE, `/`(`*`(i), `*`(`+`(m, 2))))], thickness = 2), i = 2 ...](images/Expo_0_19.gif){kind=small} |
 |
|
 |
| > |
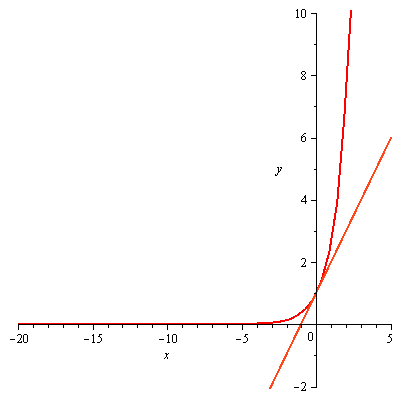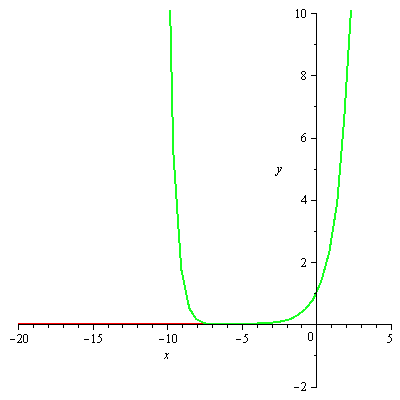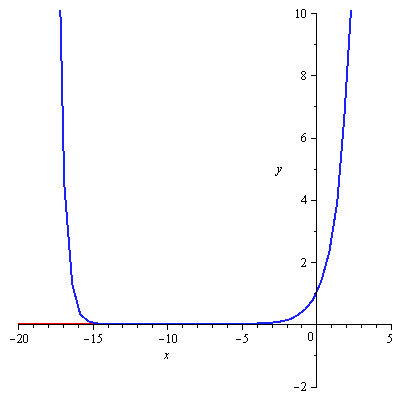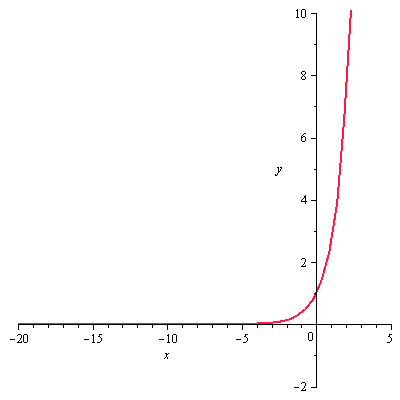
A seguir, temos uma ilustração da convergência da série para 
variando a ordem de 1 a 60.
| > | ![`assign`(m, 60); -1; `assign`(frms, seq(plot([exp(x), convert(taylor(exp(x), x, i), polynom)], x = -20 .. 5, y = -2 .. 10, color = [red, COLOR(HUE, `/`(`*`(i), `*`(`+`(m, 2))))], thickness = 2), i = 2...](images/Expo_0_23.gif){kind=small} ![`assign`(m, 60); -1; `assign`(frms, seq(plot([exp(x), convert(taylor(exp(x), x, i), polynom)], x = -20 .. 5, y = -2 .. 10, color = [red, COLOR(HUE, `/`(`*`(i), `*`(`+`(m, 2))))], thickness = 2), i = 2...](images/Expo_0_24.gif){kind=small} ![`assign`(m, 60); -1; `assign`(frms, seq(plot([exp(x), convert(taylor(exp(x), x, i), polynom)], x = -20 .. 5, y = -2 .. 10, color = [red, COLOR(HUE, `/`(`*`(i), `*`(`+`(m, 2))))], thickness = 2), i = 2...](images/Expo_0_25.gif){kind=small} ![`assign`(m, 60); -1; `assign`(frms, seq(plot([exp(x), convert(taylor(exp(x), x, i), polynom)], x = -20 .. 5, y = -2 .. 10, color = [red, COLOR(HUE, `/`(`*`(i), `*`(`+`(m, 2))))], thickness = 2), i = 2...](images/Expo_0_26.gif){kind=small} ![`assign`(m, 60); -1; `assign`(frms, seq(plot([exp(x), convert(taylor(exp(x), x, i), polynom)], x = -20 .. 5, y = -2 .. 10, color = [red, COLOR(HUE, `/`(`*`(i), `*`(`+`(m, 2))))], thickness = 2), i = 2...](images/Expo_0_27.gif){kind=small} |
 |
| > |